快速排序、堆排序、归并排序、插入排序、选择排序、冒泡排序,都是基于比较的排序方法。比较排序的下线是O(nlogn),即在最差情况下,任何一种比较排序至少需要O(nlogn)比较操作。
5个元素7次比较
先说一下,3个元素排序至少需要几次比较操作?3次!这个很简单。那么4个元素呢?5次。一种方法是按照归并排序的思想:把4个元素划分成两组,每组两个元素。每组名比较一次,那么得到两个有序的子序列(we compared 2 times),那么合并两个有序子序列,我们需要比较两个序列长度和-1次的计较操作,显然就是5次。
那现在5个元素呢?
其实,上面对于4个元素来进行归并子序列的时候,在我们比较过子序列的头两个元素后(默认子序列递增,这时候做了3次比较操作),
assumption: 1st seq : a < b and 2nd seq : c < d
we do the 3rd comparison: a & c
if a < c
we get: a < c < d, a < b
就是说,经过三次比较可以得到4个元素的某3个元素的全序关系,并且还知道另一个元素和前面3个元素中某一个的关系。
那么,对于5个元素,经过3次比较也可以得到这样的关系。这时候我们将第5个元素:\(e\),按照二分查找插入到有全序关系的3个元素中,需要2次比较操作。又因为未排好序的最后一个元素和有全序关系的4个元素中的一个已经存在关系,这样最多等于将一个新的元素插入到有全序关系的3个元素中,也是需要2次比较。能不能再少?基于比较操作,不能!因为 \(log_2(5!) = 6.91\).
一张5个元素最坏情况最少7次比较的图:
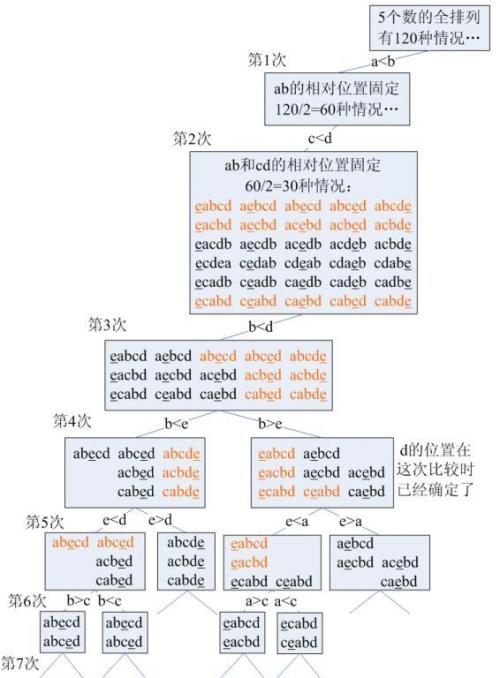
比较排序的下限
使用比较操作来对元素进行排序,实际上就是通过比较来获得元素之间的信息,获得的信息足够那么,自然就知道元素的排序了。
下面大部分内容来自很多高效排序算法的代价是 nlogn,难道这是排序算法的极限了吗? - 回答作者:舒自均
- \(n\) 个元素有 \(n!\) 种排序
- 抽两个元素 \(a\), \(b\),要么 \(a\) 比 \(b\) 大,要么 \(a\) 比 \(b\) 小,两种情况包含的可能性一共 \(n!\) 种,所以至少有一种包含了 \(\frac{n!}{2}\) 种可能性,假设每次都运气不好,留下了多的那部分
- 再抽另两个元素来比较,在剩下 \(\frac{n!}{2}\) 种可能性中,又会有少于一半的可能性被排除,于是两次比较,可能的顺序种类从 \(n!\) 下降到了(大于等于) \(\frac{n!}{4}\)
- 每比较一次,可能的顺序种类最多下降一半,于是要想让可能的顺序种类减到1(也就是排序完成),需要x次,那么必须至少有 \(2^x>n!\)。也就是经过 \(x\) 次比较,下面的分母变为 \(2^x\).
其实,这个问题类似于给一个排序,让你交换任意2个元素,最少多少次可以产生 \(n!\) 个不同的排列。那每交换两个元素会再已有可能的基础上增加一倍的可能,那么要达到 \(n!\) 种可能,则至少有 \(2^x>n!\)。
于是 \(x>log_{2}(n!)\) 后者用斯特林公式 \(n!\sim \sqrt{2\pi n} \left( \frac{n}{e} \right) ^{n}\) 自然就会得到 \(x\) 的下限和 \(nlogn\) 是同阶的。 \(n\) 很大时最多相差一个常数的倍数 快排堆排和归并,差别就在这个倍数上。但是都没有达到理论上的最优。