SVM也就是支持向量机!希望写下这个post可以加深自己的理解,因为只是看书或者看别人的博客理解并不深刻。
Support Vector Machine(SVM),是一个分类算法(也有用来作回归的)。那么对于一个二分类的问题,SVM就是要寻找到一个最优超平面将两类的样本分的最开。
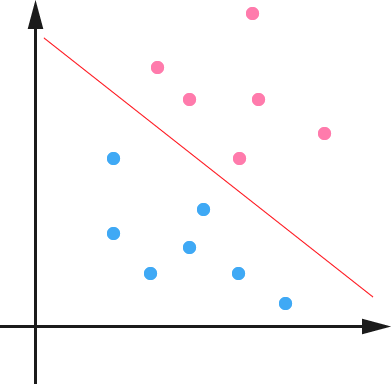
首先,两类(正类和负类)线性可分的情况下,SVM直观上和感知机是类似的,都是找到一个超平面将两类分割开来。但是,感知机找到的分割面是随机的没有分类错误的样本即停止。而SVM在线性可分的二分类问题中找到的一定是分类间隔最大的。从几何直观上看样本越接近分类超平面越难分(比如,感知机找到的超平面稍微移动一点就可能对样本分类得到相反结果),那么我们就希望样本到目标超平面的距离越远,这也正是SVM要做的。
间隔定义

函数间隔
函数间隔(functional margin)定义为\(\hat{\gamma}=y(w^Tx+b)=yf(x)\),其中\(f(x)=w^Tx+b\)就是找到的分类超平面。函数间隔可以相对的表示样本\(x\)与超平面的距离。那么如果使用SVM确定了某个二分类问题的超平面,可以使用函数间隔来对样本进行分类:如果\(w^Tx+b>0\),就将样本\(x\)分为正类,否则分为负类。直观上,如果正类的\(f(x)\)越大负类的\(f(x)\)越小,则表示样本分的越开(对于任意\(w,x\),如果可以正确将两类分开),即在样本空间中正负类非常好分。
几何间隔:
如上图所示,直线是超平面、\(x_0\)是\(x\)到超平面的垂足、\(w\)是超平面的法向量、\(\gamma\)表示\(x\)到\(x_0\)的距离,则\(\gamma\)满足:
\[x=x_0+\gamma\frac{w}{\|w\|}\]又由于\(x_0\)是超平面上的点,满足\(f(x_0)=0\),代入超平面方程可以得到:
\[\gamma = \frac{w^Tx+b}{\|w\|}=\frac{f(x)}{\|w\|}\]不过,这里的\(\gamma\)是带有符号的,我们需要的只是它的绝对值,因此也乘上对应的类别\(y\)即可:
\[\tilde{\gamma} = y\gamma = \frac{\hat{\gamma}}{\|w\|}\]这里\(\tilde{\gamma}\)就是几何间隔。之所以定义几何间隔是因为,在超平面\(w^Tx+b=0\)确定的情况下同比例的增大和缩小\(w\)与\(x\)会改变函数间隔而几何间隔则不受影响。而SVM的最大间隔也正是最大化几何间隔。
二类线性可分SVM
前提:存在一个超平面将所有样本正确分类;\(x_i\)表示样本集中第\(i\)个样本,\(y_i\in{+1, -1}\)表示样本\(i\)所属类别,这里\(+1\)表示正类,共有\(m\)个样本。
\(\exists w,b\),使得对于所有样本\(i\):
\[\begin{cases} w^Tx_i+b \geqslant +1, y_i=+1\\ w^Tx_i+b \leqslant -1, y_i=-1 \end{cases}\]上式中的\(=\)总是成立的!并且称使得等号成立的样本为支持向量。那么,在这种情况下最大的几何间隔就是$\frac{2}{|w|}$,即:
\[\max \limits_{w,b} \frac{2}{\|w\|}\] \[s.t. y_i(w^Tx_i+b) \geqslant 1, i = 1,2,..,m.\]该式等价于:
\[\min \limits_{w,b} \frac{1}{2}{\|w\|}^2\] \[s.t. y_i(w^Tx_i+b) \geqslant 1, i = 1,2,..,m. \qquad (1)\]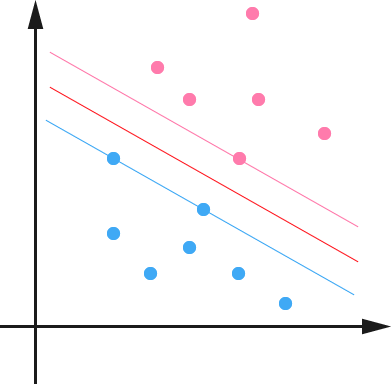
如上图所示,中间的红线是我们找到的最优分隔超平面。而超平面两侧的线上面的点(样本)就是支持向量。它们到超平面的距离相等,即求得的最大的几何间隔。
软间隔 SVM
在样本数据线性不可分的情况下,上面的约束是无解的。并且假如数据可分,但是由于噪音的影响(比如,两个噪音数据不同类别且距离特别近),我们最后得到的分类间隔就很小,那么测试误差就可能很大,也就是对噪音过拟合了。
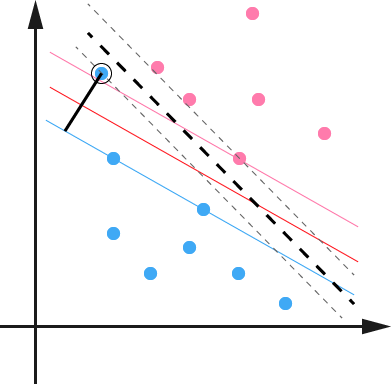
上图圈起来的蓝色点就是一个噪音(outlier)数据,由于它的存在导致超平面发生偏移,间隔变小。如果这个噪音再上移一点就没有能将数据分开的超平面。
那我们就要容忍样本在一定程度上可以偏离超平面,而样本 $x_i$ 允许偏离超平面的距离叫做松弛变量记作,$\xi_i$,也就是图中黑色实线的距离。
这样的话,原来的约束条件 $(1)$ 就便成了,
\[y_i(w^Tx_i+b) \geq 1-\xi_i, i=1,2\dots,m. \qquad (2)\]并且我们要对 $\xi_i$ 添加约束,不然 $\xi_i$ 任意大的话,是个超平面都能行。
那么,目标函数就变成了这样:
\[\begin{align} \min & \frac{1}{2}\|w\|^2 + C\sum_{i=1}^m\xi_i \\ s.t., & y_i(w^Tx_i+b)\geq 1-\xi_i, i=1,\ldots,m \\ & \xi_i \geq 0, i=1,\ldots,m \end{align}\]hinge 损失
我们知道,如果样本在超平面间隔之外,那么该样本的偏移就是 $0$.如果没有也就是说样本 $x_i$ 到超平面的距离小于 $1$,那么容忍的偏移就是 $1-y_i(w^Tx_i+b)$,即:
\[\begin{align} 1-y_i(w^Tx_i+b) &\leq 0 \longrightarrow \xi_i = 0 \\ 1-y_i(w^Tx_i+b) &\geq 0 \longrightarrow \xi_i = 1-y_i(w^Tx_i+b) \end{align}\]也就是 $\xi_i$ 取 $1-y_i(w^Tx_i+b)$ 和 $0$ 中的大者。
那么目标函数也可以写成,
\[\min_{b,w} \frac{1}{2}\|w\|^2 + C\sum_{i=1}^mmax(1-y_i(w^Tx_i+b),0)\]这也就变成了常说的损失函数+正则项的形式。
至于为什么不用 hinge loss 求解 SVM 问题(好像我这里还没有提到求解 ^o^~~~),如果是上面松弛变量的形式,她是一个关于 $w$ 的二次规划问题求解形式:目标函数是 $w,b$ 的二次项和一次项,约束都是一次项,那这种问题有很多包可以直接求解。而对于 hinge 损失这样约束也在目标函数中,或者没有一次项约束就不是一个 QP 问题,木有包包。
再一个,max 函数不可导,不用二次规划方法也不好解。
路好长,剩下的过了这段这总结~
对偶问题、KKT 条件、SMO 算法。。。
而且大数据时代 SVM+Kernel Q_Q…
160729更新