Exception Maximization in Gnernel

最大期望算法（Expectation-maximization algorithm，又叫期望最大化算法）在统计中被用于寻找，依赖（存在）于不可观察的隐性变量的概率模型中，参数的最大似然估计。

在统计计算中，最大期望(EM)算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于（存在）无法观测的隐藏变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。最大期望算法经过两个步骤交替进行计算，第一步是计算期望(E)，利用对隐藏变量的现有估计值，计算其最大似然估计值；第二步是最大化(M)，最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

---

待解决问题

假设一个概率模型，我们将所有的观测变量记作 $X=(X_1,X_2,\dots,X_n)^T$，而隐含变量记作 $Z=(Z_1,Z_2\dots,Z_n)^T$。而隐变量和观测变量的联合概率分布 $p(X,Z\mid \Theta)$ 由参数 $\Theta$ 控制。 对于高斯混合模型来说，观测变量就是样本数据，而隐变量则是样本 $x_i$ 是由哪个高斯分布产生的（这样的话，一个样本对应一个隐含变量），这个我们不清楚（但是希望估计出来概率，也就是 $\pi$）。$\Theta=\pi,\mu,\Sigma$.

假设隐变量是离散的，我们的目标函数则是最大化似然函数，

\[p(X\mid \theta)=\sum_Z p(X,Z\mid \theta) \qquad (1)\]

因为直接优化 $p(X\mid \theta)$ (incomplete-data Likelihood) 比较难，那么我们优化完整数据（complete-data:观测变量和隐变量）的似然函数。

式 $(1)$ 中 $Z$ 是一个向量，对应每个样本的隐含变量。如果隐含变量的可能取值有 $k$ 个，那么 $Z$ 就有 $k^N$ 种情况需要求和。

$Z$ 的含义困扰了我近一天，还在 stats.stackexchange.com 第一次提问，最后算是自答（添加了评论），收获了第一个 question vote. Derivation of expectation-maximization in General - PRML

和师弟的讨论不错不错:-)。

---

EM算法

因为直接优化 $ln \;p(X \mid \theta) = ln \;\sum_Z p(X,Z\mid \theta)$ 是很难的，优化 $ln \; p(X,Z\mid \theta)$ 的最大化是相对容易的（如果知道隐含变量的值，直接对参数求导为 $0$ 即可）。但是，我们对隐含变量 $Z$ 取值的知识仅仅来源于后验概率分布 $p(Z\mid X,\theta)$，因此我们考虑在隐含变量的后验概率分布下，全数据的对数似然的期望值。这也就是EM算法的E步骤，而M步骤这时最大化这个期望，这也是算法名字的由来。

In practice, however, we are not given the complete data set ${X, Z}$, but only the incomplete data $X$ Our state of knowledge of the values of the latent variables in $Z$ is given only by the posterior distribution $p(Z\mid X, \theta)$. Because we cannot use the complete-data log likelihood, we consider instead its expected value under the posterior distribution of the latent variable, which corresponds (as we shall see) to the E step of the EM algorithm.

这里，我们定义隐含变量 $Z$ 的分布 $q(Z)$.则，

\[ln\;p(X\mid \theta)=\mathcal{L}(q,\theta)+KL(q\lVert p) \qquad (2)\]

其中，

\[\begin{align} \mathcal{L}(q,\theta) &= \sum_Z q(Z)\;ln\left\{\frac{p(X,Z\mid \theta)}{q(Z)}\right\} \qquad (3) \\ KL(q\lVert p)&=-\sum_Z q(Z)\; ln\left\{ \frac{p(Z\mid X,\theta)} {q(Z)} \right\} \qquad (4) \\ &=\sum_Z q(Z)\; ln\left\{ \frac {q(Z)} {p(Z\mid X,\theta)} \right\} \qquad (4) \end{align}\]

注：由式 $(3)$ 加 $(4)$，以及 $\sum\limits_{Z} q(Z)=1$ 可得式 $(2)$.

$\mathcal{L}(q,\theta)$ 是概率分布 $q(Z)$ 的一个泛函，并且是参数 $\theta$ 的函数。值得注意的是，$(3)$ 式包含了 $X$ 和 $Z$ 的联合概率分布；而 $4$ 式则包含了给定 $X$ 的条件下，$Z$ 的概率分布（都是我们刚开始提到的）。

$(4)$ 表示 $q(Z)$ 和后验概率分布 $p(Z\mid X,\theta)$ 之间的 Kullback-Leibler散度。并且KL散度大于等于 $0$.当且仅当 $q(Z)=p(Z\mid X,\theta)$ 时等号成立。那么说 $\mathcal{L}(q,\theta) \leq ln\; p(X\mid \theta)$，即 $\mathcal{L}(q,\theta)$ 是 $p(X\mid \theta)$ 的一个下界。

分解图示：

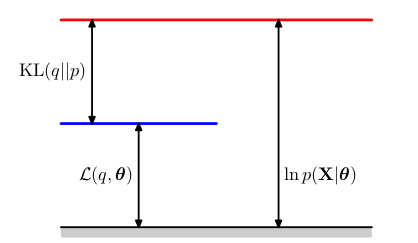
执行 EM 算法

EM算法是一个两阶段的迭代优化算法，用于寻找最大似然解。可以通过对式 $2$ 使用EM算法，来证明算法可以最大化对数损失。

在E步骤中，先固定 $\theta=\theta^{old}$. 那么式 $2$ 中，$ln\; q(X\mid \theta)$ 是一个不依赖于 $q(Z)$ 的固定值。所以 $\mathcal{L}(q,\theta)$ 的最大值出现在 $KL(q\lVert p)$ 等于 $0$ 的时候，即 $q(Z)=p(Z\mid X,\theta)$。此时的下界等于同样参数为 $\theta^{old}$ 时的对数似然函数。

在接下来的M步骤中，固定分布 $q(Z)$，下界 $\mathcal{L}(q,\theta)$ 关于 $\theta$ 进行最大化，得到新的参数 $\theta^{new}$.这会使得下界增大（除非已经到了极大值），同样会使得对数似然函数增大。并且，对数似然函数的增大量大于下界的增大量，这是由于 $\theta$ 的改变，使得KL散度不为 $0$.

如果将KL散度为 $0$ 的条件代入式 $3$ 得，

\[\begin{align} \mathcal{L}(q,\theta) &= \sum_Z p(Z\mid X,\theta^{old})ln\;p(Z\mid X,\theta)-\sum_Z p(Z\mid X,\theta^{old})ln\;p(Z\mid X,\theta^{old}) \\ & = \mathcal{Q}(\theta,\theta^{old}) + const \end{align}\]

上式后一项之所以是const，以为和此时的变量 $\theta$ 无关。而我们最大化的其实是全数据对数似然的期望，关于隐含变量后验分布的。

---

小结

EM算法最大化的是全数据关于隐含变量后验分布的对数似然。

而我们的目标函数，incomplete-data似然函数，除非算法收敛不然一直在增加，所以最大期望算法可以最大化目标似然。

---

References:

1. Expectation–maximization algorithm
2. PRML
3. 模式识别与机器学习 马春鹏

注3由于作者声明不让传播，有意请自行寻找。