损失函数 + L2正则化的极值问题,都可以用核变成一个非线性的问题。
L2正则极值问题
如果最小化问题如下所述:
\[\min \limits_{w} \frac{\lambda}{N}w^Tw + \frac{1}{N} \sum_{n=1}^N err(y_n,w^Tz_n)\]那么,$w$ 的最优解就可以表示为 $w_*=\sum_{n=1}^N \beta_n z_n$,这里 $z_n$ 可以表示原始样本空间,也可以表示经过核变换之后的空间。
证明
我们可以使得 $w_* = w_{\mid\mid}+w_{\bot}$,其中 $w_{\lVert}\in span(z_n)$ & $w_{\bot} \bot span(z_n)$,也就是说我们需要证明 $w_\bot = 0$.
\[\begin{align} &\because w_\bot^Tz_n = 0 \\ &\therefore err(y_n,w_*^Tz_n) = err(y_n,(w_\lVert + w_\bot)^Tz_n) = err(y_n,w_\lVert^Tz_n) \end{align}\]但是最小化问题的第一项 $w*$ 肯定是大于 $w_\lVert$,即:
\[w_*^Tw_*=w_\lVert^Tw_\lVert+2w_\lVert^Tw_\bot+w_\bot^Tw_\bot\]所以,如果 $w_\bot \neq 0$,$w_\lVert \; is \; more \; good.$
核 LR
L2正则逻辑回归问题:
\[\min \limits_{w} \frac{\lambda}{N}w^Tw + \frac{1}{N} \sum_{n=1}^N ln(1+exp(-y_nw^Tz_n)) \qquad (1)\]将最优解 $w_* = \sum_{n=1}^N \beta z_n$ 这样表示,那么求解 $w$ 的问题就转换成求解 $\beta$ 的问题。
\[\min \limits_{\beta} \frac{\lambda}{N} \sum_{m=1}^N \sum_{m=1}^N \beta_n \beta_m K(x_n, x_m) + \frac{1}{N} \sum_{n=1}^N ln(1+exp(-y_n \sum_{m=1}^N \beta_m K(x_m, x_n)))\]然后使用梯度下降(GD)或者 SGD 求解这个无约束问题。
注:其实,由 (1) 可以发现 LR 使用的损失函数,直接看来并不是 $0-1$ 损失函数的上限 -> log 损失:$err_{SCE}(f,y_i)=log_2(1+exp(y_if(x_i)))$,即:
$LR \;loss = ln2*err_{SCE}(f,y_i)$,但是并不影响正则化,只不过是把 $ln_2$ 转移到了 $\lambda$ 中。
核 Ridge
L2正则Ridge回归问题:
\[\min \limits_{w} \frac{\lambda}{N}w^Tw + \frac{1}{N} \sum_{n=1}^N (y_n-w^Tz_n)^2\]将最优解 $w_* = \sum_{n=1}^N \beta z_n$ 这样表示,那么求解 $w$ 的问题就转换成求解 $\beta$ 的问题。
\[\min \limits_{\beta} \frac{\lambda}{N} \sum_{m=1}^N \sum_{m=1}^N \beta_n \beta_m K(x_n, x_m) + \frac{1}{N} \sum_{n=1}^N \left(y_n - \sum_{m=1}^N \beta_m K(x_m, x_n)\right)^2 \qquad (2)\\ = \frac{\lambda}{N} \beta^TK \beta + \frac{1}{N}\left(\beta^T K^TK \beta -2\beta^T K^T y + y^TY \right) = E_{aug}(\beta)\]之所以可以快速以矩阵表示,是 $(2)$ 式第二项中平方部分可以看成向量的二范数。
\[\nabla E_{aug}(\beta) = \frac{2}{N} \left(\lambda K^TI\beta + K^TK\beta - K^Ty \right) = \frac{2}{N} K^T \left((\lambda I + K)\beta -y\right)\]令梯度为 $0$,解得 $\beta = (\lambda I + K)^{-1}y$,因为核矩阵是半正定,所以逆矩阵存在。但是,时间复杂度是 $O(N^3)$,而且矩阵是稠密矩阵,对于大数据(样本巨多)时间复杂度求逆太高。
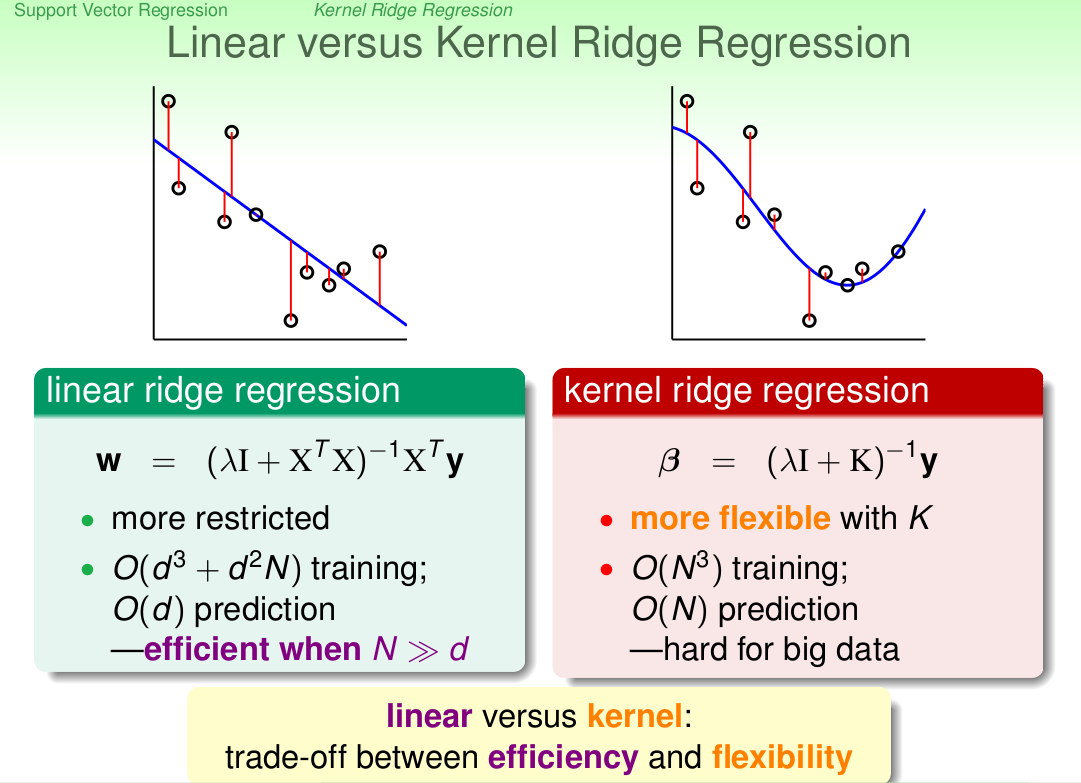
下面这时岭回归与核岭回归的比较: